Understanding the function surf() in Octave/MATLAB

I’ve been studying Machine Learning for a few days now, on Coursera. After finishing 1^st and 2^nd weeks, I’ve got the first assignment for the course where you are supposed to implement Linear Regression using Gradient Descent.

While trying to do the assignment, I’ve come across with a function, surf(), for which I’ve struggled a few hours a little bit to understand.

---

What was confusing for me in the assignment was this line below:

Because of the way meshgrids work in the surf() command, we need to transpose J_vals before calling surf, or else the axes will be flipped. J_vals = J_vals';

I couldn’t get that at first glance, so I’ve started fiddling with the function and plots until a few hours later I’ve found this explanation from the docs¹.

If x and y are vectors, then a typical vertex is (x(j), y(i), z(i,j)). Thus, columns of z correspond to different x values and rows of z correspond to different y values.

Take home message: Always check for the docs FIRST. ¯_(ツ)_/¯

---

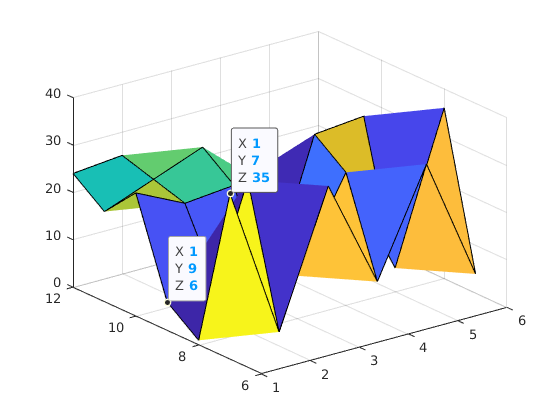
Anyway, to visualize this I’ve plotted a graph using the code below:

A = [1 2 3 4 5 6];
B = [7 8 9 10 11 12];
C = magic(6);

% Matrix C:
% 35  1   6   26   19   24
% 3   32  7   21   23   25
% 31  9   2   22   27   20
% 8   28  33  17   10   15
% 30  5   34  12   14   16
% 4   36  29  13   18   11

surf(A, B, C)

By the way, I should mention that in the assignment we were assigning the elements of the matrix C (which corresponds to J_vals in the snippet below) like:

% theta0_vals is a 1x100 row vector, which in our case is the matrix A
% theta1_vals is a 1x100 row vector, which in our case is the matrix B
for i = 1:length(theta0_vals)
    for j = 1:length(theta1_vals)
	  t = [theta0_vals(i); theta1_vals(j)];
	  J_vals(i,j) = computeCost(X, y, t);
    end
end

In the above code, we are assigning the result of the computation from A_i and B_j to C_i,j.

So you can think of it as C_i,j = (A_i, B_j).

Considering the explanation above, after using surf(A, B, C) you might think that C(A(1), B(3)) which is C(1,9) should be equal to C_1,3 which is 6.

But as you can see from the above surface plot, the point (1, 9) maps to 31 or you can use interp2(A, B, C, 1, 9) which will give you the same result.

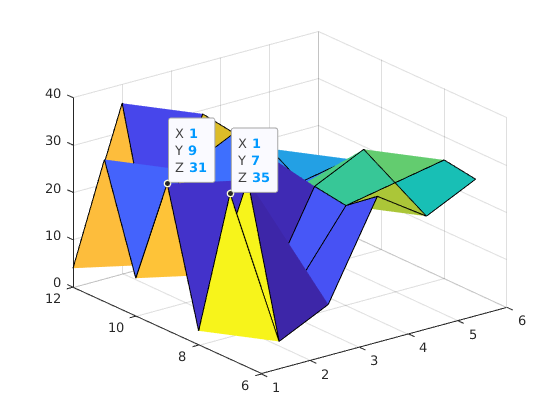
Hence, we take the transpose of the matrix C:

surf(A, B, C')

to get :

References